UNIT-I

Algorithm Analysis:-

Algorithm Analysis: Introduction to Algorithm, Algorithm Analysis, Asymptotic Notations. Introduction to arrays and Abstract Data Type (ADT) Lists: List using arrays and linked list- Singly Linked List, Doubly Linked List, Circular Linked List.

Introduction to Algorithm

Algorithm Definition: - An algorithm is a set of instructions that are used to solve a problem. (Or) An algorithm is a Step By Step process to solve a problem, where each step indicates an intermediate task. Algorithm contains finite number of steps that leads to the solution of the problem.

Properties/Characteristics of an algorithm:-

Algorithm has the following basic properties

1. Input: - An algorithm has zero (0) or more inputs.

2. Output: - An algorithm must produce one (1) or more outputs.

3. Finiteness:-An algorithm must contain a finite/countable number of steps.

4. Definiteness: - Each step of an algorithm must be stated clearly and unambiguously.

5. Effectiveness: - An algorithm should be effective i.e. operations can be performed with the given inputs in a finite period of time by a person using paper and pencil.

Categories of Algorithm:

Based on the different types of steps in an Algorithm, it can be divided into three categories, namely

 Sequence

 Selection and

 Iteration

Sequence: The steps described in an algorithm are performed successively one by one without skipping any step. The sequence of steps defined in an algorithm should be simple and easy to understand. Each instruction of such an algorithm is executed, because no selection procedure or conditional branching exists in a sequence algorithm.

Example:

// adding two numbers

Step 1: start

Step 2: read a,b

Step 3: Sum=a+b

Step 4: write Sum

Step 5: stop

Selection: The sequence type of algorithms are not sufficient to solve the problems, which involves decision and conditions. In order to solve the problem which involve decision making or option selection, we go for Selection type of algorithm. The general format of Selection type of statement is as shown below:

if(condition)

Statement-1;

else

Statement-2;

The above syntax specifies that if the condition is true, statement-1 will be executed otherwise statement-2 will be executed. In case the operation is unsuccessful. Then sequence of algorithm should be changed/ corrected in such a way that the system will re-execute until the operation is successful.

Iteration: Iteration type algorithms are used in solving the problems which involves repetition of statement. In this type of algorithms, a particular number of statements are repeated ‘n’ no. of times.

Example1:

• Example1:

• Step 1 : start

• Step 2 : initialize variables.

• Step 3 : check for condition

• Step 4 : if the condition is true, then go to step5 otherwise goto step7.

• Step 5 : f=f*i

• Step 6 : goto step3

• Step7 : print value of factorial f

• Step8 : stop

Performance Analysis (or) Analysis of an algorithm

Analysis of algorithm is the task of determining how much computing time (Time complexity) and storage (Space complexity) required by an algorithm.

We can analyze performance of an algorithm using Time complexity and Space complexity.

Time Complexity: - The amount of time that an algorithm requires for its execution is known as time complexity.

Time complexity is mainly classified into 3 types.

1. Best case time complexity

2. Worst case time complexity

3. Average case time complexity

1. Best case time complexity: - If an algorithm takes minimum amount of time for its execution then it is called as Best case time complexity.

Ex: - While searching an element using linear search, if key element found at first position then it is best case.

2. Worst case time complexity: - If an algorithm takes maximum amount of time for its execution then it is called as Worst case time complexity.

Ex: - While searching an element using linear search, if key element found at last position then it is worst case.

3. Average case time complexity: - If an algorithm takes average amount of time for its execution then it is called as Average case time complexity.

Ex: - While searching an element using linear search, if key element found at middle position then it is average case.

There are 2 types of computing times.

1. Compilation time

2. Execution time or run time

· The time complexity is generally calculated using execution time or run time.

· It is difficult to calculate time complexity using clock time because in a multiuser system, the execution time depends on many factors such as system load, number of other programs that are running.

· So, time complexity is generally calculated using Frequency count (step count) and asymptotic notations.

Frequency count (or) Step count:-

It denotes the number of times a statement to be executed.

Generally count value will be given depending upon corresponding statements.

· For comments, declarations the frequency count is zero (0).

· For Assignments, return statements the frequency count is 1.

· Ignore lower order exponents when higher order exponents are present.

· Ignore constant multipliers.

Ex: - A sample program to calculate time complexity of sum of cubes of ‘n’ natural numbers.

int sum(int n) --------------------0

{ --------------------0

int i,s; --------------------0

s=0; --------------------1

for(i=1;i<=n;i++) --------------------(n+1)

s=s+i*i*i; --------------------n

return s; --------------------1

}

______

2n+3

______

So, time complexity=O(n)

General rules or norms for calculating time complexity:-

Rule 1:-The running time of for loop is the running time of statements in for loop.

Ex:- for(i=0;i<n;i++) -----------(n+1)

s=s+i; ------------ n

__________

2n+1

__________

So, time complexity=O(n)

Rule 2:-The total running time of statements inside a group of nested loops is the product of the sizes of all loops.

Ex:- for(i=0;i<n;i++) ---------------- (n+1)

for(j=0;j<n;j++) ---------------- n(n+1)

c[i][j]=a[i][j]+b[i][j]; ------------- (n*n)

_____________

2n²+2n+1

_____________

So, time complexity=O(n²)

Rule 3:-The running time is the maximum one.

Ex:- for(i=0;i<n;i++) ----------- (n+1)

a[i]=0; ----------- n

for(i=0;i<n;i++) ------------ (n+1)

for(j=0;j<n;j++) ------------ n(n+1)

a[i]=a[i]+a[j]+i+j; ------------- n²

____________

2n²+4n+2

____________

So, time complexity=O(n²)

Rule 4:- if-else

if(cond)

else

Here running time is maximum of running times of s1 and s2.

Ex:- int sum(int n) -------------- 0

{ --------------- 0

int s,i; -------------- 0

s=0; -------------- 1

if(n<=0) -------------- 1

return n; ------------- 1

else ------------- 0

{ ------------- 0

for(i=0;i<n;i++) -------- n+1

s=s+i; ---------- n

return s; ----------- 1

}

____________

2n+5

__________________

So, time complexity=O(n)

What is Space complexity?

When we design an algorithm to solve a problem, it needs some computer memory to complete its execution. For any algorithm, memory is required for the following purposes...

To store program instructions.
To store constant values.
To store variable values.
And for few other things like funcion calls, jumping statements etc,.

Space complexity of an algorithm can be defined as follows...

Total amount of computer memory required by an algorithm to complete its execution is called as space complexity of that algorithm.

Generally, when a program is under execution it uses the computer memory for THREE reasons. They are as follows...

Instruction Space: It is the amount of memory used to store compiled version of instructions.
Environmental Stack: It is the amount of memory used to store information of partially executed functions at the time of function call.
Data Space: It is the amount of memory used to store all the variables and constants.

Note - When we want to perform analysis of an algorithm based on its Space complexity, we consider only Data Space and ignore Instruction Space as well as Environmental Stack.
That means we calculate only the memory required to store Variables, Constants, Structures, etc.,

To calculate the space complexity, we must know the memory required to store different datatype values (according to the compiler). For example, the C Programming Language compiler requires the following...

2 bytes to store Integer value.
4 bytes to store Floating Point value.
1 byte to store Character value.
6 (OR) 8 bytes to store double value

Consider the following piece of code...

Example 1

int square(int a)

{

return a*a;

}

In the above piece of code, it requires 2 bytes of memory to store variable 'a' and another 2 bytes of memory is used for return value.

That means, totally it requires 4 bytes of memory to complete its execution. And this 4 bytes of memory is fixed for any input value of 'a'. This space complexity is said to be Constant Space Complexity.

Example 2

int sum(int A[ ], int n)

   int sum = 0, i;

   for(i = 0; i < n; i++)

      sum = sum + A[i];

   return sum;

n*2' bytes of memory to store array variable 'a[ ]'

2 bytes of memory for integer parameter 'n'

4 bytes of memory for local integer variables 'sum' and 'i' (2 bytes each)

2 bytes of memory for return value.

That means, totally it requires '2n+8' bytes of memory to complete its execution. Here, the total amount of memory required depends on the value of 'n'. As 'n' value increases the space required also increases proportionately. This type of space complexity is said to be Linear Space Complexity.

If the amount of space required by an algorithm is increased with the increase of input value, then that space complexity is said to be Linear Space Complexity

Asymptotic notations

Asymptotic notations are used to calculate time complexity of algorithm.

Using asymptotic notations we can calculate best case, worst case and average case time complexity.

There are 5 types of time complexities.

1. Big Oh notation (O)

2. Big Omega notation (Ω)

3. Theta notation (θ)

4. Little Oh notation (o)

5. Little omega notation (ω)

1. Big Oh notation (O):-

· It is a method of representing upper bound of algorithm’s running time.

· Using Big Oh notation we can calculate maximum amount of time taken by an algorithm for its execution.

· So, Big Oh notation is useful to calculate worst case time complexity.

Definition: - Let f(n) , g(n) be 2 non negative functions. Then f(n)=O(g(n)), if there are 2 positive constants c, n₀ such that f(n)<=c*g(n) ∀ n>=n₀.

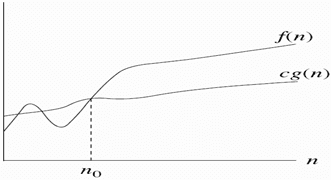
Graphical representation of Big Oh notation(O):-

Ex:- f(n)=3n+2

g(n)=n;

To show f(n)=O(g(n))

f(n)<=c*g(n) , c>0, n₀>=1

3n+2<=c*n

Let C=4, n₀=1 then 5<=4 wrong

n₀=2 then 8<=8 correct

n₀=3 then 11<=12 correct

n₀=4 then 14<=16 correct

So, n₀>=2

Hence, 3n+2<=4*n ∀ n>=2

2. Big Omega notation (Ω):-

· It is a method of representing lower bound of algorithm’s running time.

· Using Big Omega notation we can calculate minimum amount of time taken by an algorithm for its execution.

· So, Big Omega notation is useful to calculate best case time complexity.

Definition: - Let f(n) , g(n) be 2 non negative functions. Then f(n)= Ω (g(n)), if there are 2 positive constants c, n₀ such that f(n)>=c*g(n) ∀ n>=n₀.

Graphical representation of Big Omega notation(Ω)

f(n)= Ω (g(n))

Ex:- f(n)=3n+2

g(n)=n;

To show f(n)= Ω(g(n))

f(n)>=c*g(n) , c>0, n₀>=1

3n+2>=c*n

Let C=1, n₀=1 then 5>=1 correct

n₀=2 then 8>=2 correct

n₀=3 then 11>=3 correct

So, n₀>=1

Hence, 3n+2>=1*n ∀ n>=1

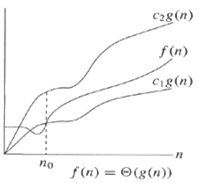
3. Theta notation (θ):-

· It is a method of representing an algorithm’s running time between upper bound and lower bound.

· Using Theta notation we can calculate average amount of time taken by an algorithm for its execution.

· So, Theta notation is useful to calculate average case time complexity.

Definition: - Let f(n) , g(n) be 2 non negative functions. Then f(n)= θ (g(n)), if there are 3 positive constants c₁, c₂,n₀ such that c₁*g(n)<=f(n)<=c₂*g(n) ∀ n>=n₀.

Graphical representation of Theta notation(O):-

Ex:- f(n)=3n+2

g(n)=n;

To show f(n)= θ(g(n))

c₁*g(n)<=f(n)<=c₂*g(n), c₁>0,

c₂>0

n₀>=1

c_1*n<=3n+2<= c₂*n

c₂=4 , c₁₌1_,

Let n₀=1 then 1<=5<=4 wrong

Let n₀=2 then 2<=8<=8 correct

Let n₀=3 then 3<=11<=12 correct

Let n₀=4 then 4<=14<=16 correct

So, n₀>=2

Hence, 1*n<=3n+2<=*4n n>=2

4. Little oh notation(o):-

For a given function g(n), ω(g(n)) is the set of functions f(n) where there exist c, n0 > 0 such that 0 < f(n) < cg(n)∀n ≥ n0.

5. Little Omega notation(ω):-

For a given function g(n), ω(g(n)) is the set of functions f(n) where there exist c, n0 > 0 such that 0 < cg(n) > f(n)∀n ≥ n0.

Various types of computing times or typical growth rates:-

O(1) à constant computing time

O(n) à linear computing time

O(n²) àQuadratic computing time

O(n³) àCubic computing time

O(2ⁿ) àExponential computing time

O(log n) à Logarithmic computing time

O(n log n) àLogarithmic computing time

N	n²	n³	2ⁿ	logn	nlogn
1	1	1	2	0	0
2	4	8	4	1	2
4	16	64	16	2	8
8	64	512	256	3	24

The relation among various computing times is,

O(logn)<O(n)<O(nlogn)<O(n²)<O(2ⁿ)<O(n³)

Definition of Data Structure:-

Data Structure is a way of Organizing data in a computer so that we can perform operations on these data in a effective way.

A data structure is basically a group of data elements that are put together under one name, and which defines a particular way of storing and organizing data in a computer so that it can be used efficiently.

Data structures are used in almost every program or software system. Some common examples of data structures are arrays, linked lists, queues, stacks, binary trees, and hash tables.

Data structures are widely applied in the following areas:

 Compiler design

 Operating system

 Statistical analysis package

 DBMS

 Numerical analysis

 Simulation

 Artificial intelligence

 Graphics

When selecting a data structure to solve a problem, the following steps must be performed.

1. Analysis of the problem to determine the basic operations that must be supported. For example, basic operation may include inserting/deleting/searching a data item from the data structure.

2. Quantify the resource constraints for each operation.

3. Select the data structure that best meets these requirements.

This three-step approach to select an appropriate data structure for the problem at hand supports a data-centred view of the design process. In the approach, the first concern is the data and the operations that are to be performed on them. The second concern is the representation of the data, and the final concern is the implementation of that representation.

Classification of Data Structures:

Data structures are generally categorized into two classes: primitive and non-primitive data structures.

1. Primitive Data Structures:

Primitive data structures are the fundamental data types which are supported by a programming language. Some basic data types are integer, real, character and Boolean. The terms ‘data type’, ‘basic data type’ and ‘primitive data type’ are often used interchangeably.

2. Non-Primitive Data Structures:

Non-primitive data structures are those data structures which are created using primitive data structures. Examples of such data structures include linked lists, stacks, trees, and graphs. Non-primitive data structures can further be classified into two categories: linear and non-linear data structures.

Linear and Non-linear Data Structures:

a) Linear Data Structure:

Linear data structures organize their data elements in a linear fashion, where data elements are attached one after the other. Linear data structures are very easy to implement, since the memory of the computer is also organized in a linear fashion. Some commonly used linear data structures are arrays, linked lists, stacks and queues.

b) Non-linear data structures: In nonlinear data structures, data elements are not organized in a sequential fashion. Data structures like multidimensional arrays, trees, graphs, tables and sets are some examples of widely used nonlinear data structures.

Operations on the Data Structures:

Following operations can be performed on the data structures:

1. Traversing- It is used to access each data item exactly once so that it can be processed.

2. Searching- It is used to find out the location of the data item if it exists in the given collection of data items.

3. Inserting- It is used to add a new data item in the given collection of data items.

4. Deleting- It is used to delete an existing data item from the given collection of data items.

5. Sorting- It is used to arrange the data items in some order i.e. in ascending or descending order in case of numerical data and in dictionary order in case of alphanumeric data.

6. Merging- It is used to combine the data items of two sorted files into single file in the sorted form.

Introduction to Arrays and Abstract Data Type(ADT)

ARRAYS

An array is a collection of similar data elements. These data elements have the same data type. The elements of the array are stored in consecutive memory locations and are referenced by an index (also known as the subscript).

In C, arrays are declared using the following,

syntax: datatype name [size];

For example,

int marks [10];

The above statement declares an array marks that contains 10 elements. In C, the array index starts from zero. This means that the array marks will contain 10 elements in all.

The first element will be stored in marks [0], second element in marks [1], so on and so forth.

Therefore, the last element, that is the 10th element, will be stored in marks [9]. In the memory, the array will be stored as shown in Fig. 1.1.

Arrays are generally used when we want to store large amount of similar type of data.

But they have the following limitations:

 Arrays are of fixed size.

 Data elements are stored in contiguous memory locations which may not be always available.

 Insertion and deletion of elements can be problematic because of shifting of elements from their positions.

Abstract Data Types

An abstract data type (ADT) is a set of operations. An ADT specifies what is to be done but how it is done is not specified i.e. all the implementation details are hidden.

The basic idea is that the implementation of these operations is written once in the program and any other part of the program that needs to perform an operation on the ADT can do so by calling the appropriate function.

For Example, stack ADT have operations like push, pop but stack ADT doesn’t provide any implementation details regarding operations.

List ADT:- List is basically a collection of elements. For example list is of the following form

A₁,A₂,A₃,- - - - -,A_n where A₁is the first element of the list

A_n is the last element of the list.

The size of the list is ‘n’. If the list size is zero (0) then the corresponding list is called as empty list.

Implementation of list:- List is implemented in 2 ways.

1. Implementation of list using arrays

2. Implementation of list using Linked list (or) Implementation of list using pointers

1.Implementation of list using arrays:- An array can be defined as a collection of similar( homogeneous ) data type elements and all the elements will be stored in contiguous ( Adjacent ) memory locations.

Array Operations:- We can perform mainly the following operations on arrays.

1. Create

2. Display (or) Traversing (or) Printing

3. Insertion

4. Deletion

5. Updation

6. Searching

7. Sorting

8. Merging

C program to implement various operations on list using Arrays:-

#include<stdio.h>

#include<conio.h>

void create();

void display();

void insertion();

void deletion();

void updation();

void search();

void sort();

void merge();

int a[10],n,i,pos,value,j,k;

void main()

{

int ch;

clrscr();

printf("\n1.Create\n2.Display\n3.Inertion\n4.Deletion\n5.Updation\n6.Search\n7.Sort\n8.Merge");

while(1)

{

printf("\nEnter your choice\n");

scanf("%d",&ch);

switch(ch)

{

case 1:create();

break;

case 2:display();

break;

case 3:insertion();

break;

case 4:deletion();

break;

case 5:updation();

break;

case 6:search();

break;

case 7:sort();

break;

case 8:merge();

break;

default:exit(1);

}

getch();

}

void create()

{

printf("\nEnter size of the array\n");

scanf("%d",&n);

printf("\nEnter elements of the array\n");

for(i=0;i<n;i++)

scanf("%d",&a[i]);

}

void display()

{

printf("\nElements of the array are\n");

for(i=0;i<n;i++)

printf("%d\t",a[i]);

}

void insertion()

{

printf("\nenter the element to be inserted");

scanf("%d",&value);

printf("\nenter the position at which the element is inserted\n");

scanf("%d",&pos);

n++;

for(i=n-1;i>pos;i--)

a[i]=a[i-1];

a[pos]=value;

}

void deletion()

{

printf("\nEnter the position at which the element is deleted\n");

scanf("%d",&pos);

n--;

for(i=pos;i<n;i++)

a[i]=a[i+1];

}

void updation()

{

printf("\nEnter the position at which the element is updated\n");

scanf("%d",&pos);

printf("\nEnter the element to be updated\n");

scanf("%d",&value);

a[pos]=value;

}

void search()

{

int key,flag=0;

printf("\nEnter key element\n");

scanf("%d",&key);

for(i=0;i<n;i++)

{

if(a[i]==key)

{

flag=1;

break;

}

if(flag==1)

printf("Key element is found");

else

printf("key element is not found");

}

void sort()

{

int temp;

for(i=0;i<n-1;i++)

{

for(j=i+1;j<n;j++)

{

if(a[i]>a[j])

{

temp=a[i];

a[i]=a[j];

a[j]=temp;

}

void merge()

{

int b[5],c[10],n1;

printf("\nEnter size of 2nd array\n");

scanf("%d",&n1);

printf("\nEnter elements of 2nd array\n");

for(j=0;j<n1;j++)

scanf("%d",&b[j]);

for(i=0,k=0;i<n;i++,k++)

c[k]=a[i];

for(j=0;j<n1;j++,k++)

c[k]=b[j];

printf("\nAfter merging the elements of array are\n");

for(k=0;k<n+n1;k++)

printf("%d\t",c[k]);

}

Advantages of Arrays:-

Array conations a collection of similar data type elements.
Array allows random access of elements i.e. an array element can be randomly accessed using index value. Arrays are simple and easy to implement.
Arrays are suitable when the number of elements are already known.
Arrays can be used to implement data structures like stacks, queues and so on.

Drawbacks of Arrays:-

We must know in advance regarding how many elements are to be stored in array.
Arrays uses static memory allocation i.e. memory will be allocated at compilation time. So it’s not possible to change size of the array at run time.
Since array size is fixed, if we allocate more memory than required then memory space will be wasted.
If we allocate less memory than required it will creates a problem.
The main drawback of arrays is insertion and deletion operations are expensive.
For example to insert an element into the array at beginning position, we need to shift all array elements one position to the right in order to store a new element at beginning position.

a[0] a[1] a[2] a[3] a[4]

11 22 33 44 55 Let value=100

a[0] a[1] a[2] a[3] a[4] a[5]

100 11 22 33 44 55

For example to delete an element from the array at beginning position , we need to shift all array elements one position to its left.

a[0] a[1] a[2] a[3] a[4]

11 22 33 44 55

a[0] a[1] a[2] a[3]

22 33 44 55

Because of the above limitations simple arrays are not used to implement lists.

Lists using arrays and linked lists

Introduction to linked lists:

A linked list, in simple terms, is a linear collection of data elements. These data elements are called nodes. Linked list is a data structure which in turn can be used to implement other data structures. Thus, it acts as a building block to implement data structures such as stacks, queues, and their variations. A linked list can be perceived as a train or a sequence of nodes in which each node contains one or more data fields and a pointer to the next node.

Linked list is a collection of nodes which are not necessary to be in adjacent memory locations.

Each node contains 2 fields.

1. Data Field

2. Next field ( or ) pointer field ( or ) address field

Data field:- Data field contains values like 9, 6.8, ‘a’ , “ramu” , 9849984900

Next field:- It contains address of its next node. The last node next field contains NULL which indicates end of the linked list.

Diagrammatic representation of linked list:-

NULL

2000

3000

1000 2000 3000

we can see a linked list in which every node contains two parts, an integer and a pointer to the next node. The left part of the node which contains data may include a simple data type, an array, or a structure. The right part of the node contains a pointer to the next node (or address of the next node in sequence).

The last node will have no next node connected to it, so it will store a special value called NULL. Hence, a NULL pointer denotes the end of the list. Since in a linked list, every node contains a pointer to another node which is of the same type, it is also called a self-referential data type.

Linked lists contain a pointer variable START that stores the address of the first node in the list. We can traverse the entire list using START which contains the address of the first node; the next part of the first node in turn stores the address of its succeeding node. Using this technique, the individual nodes of the list will form a chain of nodes. If START = NULL, then the linked list is empty and contains no nodes.

In C, we can implement a linked list using the following code:

struct node

{

int data;

struct node * next;

};

Note: Linked lists provide an efficient way of storing related data and perform basic operations such as insertion, deletion, and updation of information at the cost of extra space required for storing address of the next node.

Types of linked list:-

1. Single linked list (or) singly linked list

2. Double linked list (or) Doubly linked list

3. Circular linked list

Single linked list (or) singly linked list

A single linked list is the simplest type of linked list in which every node contains some data and a pointer to the next node of the same data type. By saying that the node contains a pointer to the next node, we mean that the node stores the address of the next node in sequence. A single linked list allows traversal of data only in one way/one direction (forward direction).

A single linked list is a collection of nodes which are not necessary to be in adjacent memory locations.

Each node contains 2 fields.

1. Data Field

2. Next field ( or ) pointer field ( or ) address field

Data field:- Data field contains values like 9, 6.8, ‘a’ , “ramu” , 9849984900

Next field:- It contains address of its next node. The last node next field contains NULL which indicates end of the linked list.

Diagrammatic representation of linked list:-

NULL

2000

3000

1000 2000 3000

It is called as single linked list because each node contains a single link which points to its next node.

Single Linked list operations:-

We can perform mainly the following operations on single linked list.

1. Creation

2. Display

3. Inserting an element into the list at begin position

4. Inserting an element into the list at end position

5. Inserting an element into the list at specified position

6. Deleting an element from the list at begin position

7. Deleting an element from the list at end position

8. Deleting an element from the list at specified position

9. Searching for a value in a linked list

10. Counting the number of elements or nodes

11. Sorting a list

11. Reversing a list

12. Merging of 2 lists

Algorithm: Traverse/Display:

Step 1: [INITIALIZE] SET POINTER TEMP = HEAD

Step 2: Repeat Steps 3 and 4 while TEMP != NULL

Step 3: Apply process to TEMP -> DATA

Step 4: SET TEMP = TEMP->NEXT

[END OF LOOP]

Step 5: EXIT

Inserting Elements to a Linked List:

We will see how a new node can be added to an existing linked list in the following cases.

1. The new node is inserted at the beginning.

2. The new node is inserted at the end.

3. The new node is inserted after a given node.

1. Insert a Node at the beginning of a Linked list:

Consider the linked list shown in the figure. Suppose we want to create a new node with data 24 and add it as the first node of the list. The linked list will be modified as follows.

· Allocate memory for new node and initialize its DATA part to 24.

· Add the new node as the first node of the list by pointing the NEXT part of the new node to HEAD.

· Make HEAD to point to the first node of the list.

Algorithm: InsertAtBeginning

Step 1: IF AVAIL = NULL

Write OVERFLOW

Go to Step 7

[END OF IF]

Step 2: SET NEW_NODE = AVAIL

Step 3: SET AVAIL = AVAIL -> NEXT

Step 4: SET NEW_NODE -> DATA = VAL

Step 5: SET NEW_NODE -> NEXT = HEAD

Step 6: SET HEAD = NEW_NODE

Step 7: EXIT

Note that the first step of the algorithm checks if there is enough memory available to create a new node. The second, and third steps allocate memory for the new node.

This algorithm can be implemented in C as follows:

struct node *new_node;

new_node = (struct node*) malloc(sizeof(struct node));

new_node->data = 24;

new_node->next = head;

head = new_node;

2. Insert a Node at the end of a Linked list:

Take a look at the linked list in the figure. Suppose we want to add a new node with data 24 as the last node of the list. Then the linked list will be modified as follows.

· Allocate memory for new node and initialize its DATA part to 24.

· Traverse to last node.

· Point the NEXT part of the last node to the newly created node.

· Make the value of next part of last node to NULL.

Algorithm: InsertAtEnd

Step 1: IF AVAIL = NULL

Write OVERFLOW

Go to Step 10

[END OF IF]

Step 2: SET NEW_NODE = AVAIL

Step 3: SET AVAIL = AVAIL -> NEXT

Step 4: SET NEW_NODE -> DATA = VAL

Step 5: SET NEW_NODE -> NEXT = NULL

Step 6: SET TEMP = HEAD

Step 7: Repeat Step 8 while TEMP -> NEXT != NULL

Step 8: SET TEMP = TEMP -> NEXT

[END OF LOOP]

Step 9: SET TEMP -> NEXT = NEW_NODE

Step 10: EXIT

This can be implemented in C as follows,

struct node *new_node;

new_node = (struct node*) malloc(sizeof(struct node));

new_node->data = 24;

new_node->next = NULL;

struct node *temp = head;

while(temp->next != NULL){

temp = temp->next;

}

temp->next = new_node;

3. Insert a Node after a given Node in a Linked list:

The last case is when we want to add a new node after a given node. Suppose we want to add a new node with value 24 after the node having data 9. These changes will be done in the linked list.

· Allocate memory for new node and initialize its DATA part to 24.

· Traverse the list until the specified node is reached.

· Change NEXT pointers accordingly.

Algorithm: InsertAnElementAtSpecificLocation

Step 1: IF AVAIL = NULL

Write OVERFLOW

Go to Step 12

[END OF IF]

Step 2: SET NEW_NODE = AVAIL

Step 3: SET AVAIL = AVAIL -> NEXT

Step 4: SET NEW_NODE -> DATA = VAL

Step 5: SET TEMP = HEAD

Step 6: SET POSITION VALUE

Step 7: Repeat Step 7 UNTIL TEMP REACHES TO POS-1 LOCATION

Step 8: Step 9: SET TEMP = TEMP -> NEXT

[END OF LOOP]

Step 9 : SET NEW_NODE -> NEXT = TEMP->NEXT

Step 10: TEMP -> NEXT = NEW_NODE

Step 11: EXIT

Deleting Elements from a Linked List

Let’s discuss how a node can be deleted from a linked listed in the following cases.

1. The first node is deleted.

2. The last node is deleted.

3. The node after a given node is deleted.

1. Delete a Node from the beginning of a Linked list:

Suppose we want to delete a node from the beginning of the linked list. The list has to be modified as follows:

· Check if the linked list is empty or not. Exit if the list is empty.

· Make HEAD points to the second node.

· Free the first node from memory.

Algorithm: DeleteFromBeginning

Step 1: IF HEAD = NULL

Write UNDERFLOW

Go to Step 5

[END OF IF]

Step 2: SET TEMP = HEAD

Step 3: SET HEAD = HEAD -> NEXT

Step 4: FREE TEMP

Step 5: EXIT

This can be implemented in C as follows,

if(head == NULL)

{

printf("Underflow");

}

else

{

temp = head;

head = head -> next;

free(temp);

}

2. Delete last Node from a Linked list:

Suppose we want to delete the last node from the linked list. The linked list has to be modified as follows:

· Traverse to the end of the list.

· Change value of next pointer of second last node to NULL.

· Free last node from memory.

Algorithm: DeleteFromEnd

Step 1: IF HEAD = NULL

Write UNDERFLOW

Go to Step 8

[END OF IF]

Step 2: SET TEMP = HEAD

Step 3: Repeat Steps 4 and 5 while TEMP -> NEXT != NULL

Step 4: SET TEMP = TEMP -> NEXT

[END OF LOOP]

Step 5: SET D = TEMP -> NEXT

Step 6: SET TEMP -> NEXT = NULL

Step 7: FREE D

Step 8: EXIT

Here we use two pointers TEMP and D to access the last node and the second last node. This can be implemented in C as follows,

if(head == NULL)

{

printf("Underflow");

}

else

{

struct node* temp = head;

while(temp->next!=NULL){

temp = temp->next;

}

d = temp->next;

temp->next = NULL;

free(d);

}

3. Delete the Node after a given Node in a Linked list:

Suppose we want to delete the that comes after the node which contains data 9.

· Traverse the list upto the specified node.

· Change value of next pointer of previous node(9) to next pointer of current node(10).

Algorithm: DeleteAfterANode

Step 1: IF HEAD = NULL

Write UNDERFLOW

Go to Step 10

[END OF IF]

Step 2: SET TEMP = HEAD

Step 3: Repeat Steps 4 UNTIL TEMP reaches to POS-1 location

Step 4: SET TEMP = TEMP -> NEXT

[END OF LOOP]

Step 5: SET D = TEMP -> NEXT

Step 6: SET TEMP -> NEXT = D -> NEXT

Step 7: SET D -> NEXT = NULL

Step 8: FREE D

Step 9 : EXIT

Implementation in C takes the following form:

if(head == NULL)

{

printf("Underflow");

}

else

{

int pos;

struct node* temp = head;

for(int i=1; i<p-1; i++){

temp = temp->next;

}

d = temp -> next;

temp -> next = d -> next;

d -> next = NULL;

free(d); }

C program to implement various operations on list using Linked list:- ( OR )

C program to implement various operations on list using Pointers:-

#include<stdio.h>

#include<stdlib.h>

void create();

void display();

void insert_at_begin();

void insert_at_end();

void insert_at_pos();

void delete_at_begin();

void delete_at_end();

void delete_at_pos();

void search();

void sort();

void count();

void reverse();

void merge();

int i,value,p;

char ch;

struct node

{

int data;

struct node *next;

}*new,*head,*temp,*d,*new1,*temp1;

void main()

{

int n;

printf("\n 1.create\n 2.display\n 3.insert-at-begin\n 4.insert-at-end\n 5.insert-at-pos\n 6.delete-at-begin\n 7.delete-at-end\n 8.delete-at-pos\n 9.search\n 10.sort\n 11.count\n 12.reverse\n 13.merge");

while(1)

{

printf("\n enter your choice:");

scanf("%d",&n);

switch(n)

{

case 1: create();

break;

case 2: display();

break;

case 3: insert_at_begin();

break;

case 4: insert_at_end();

break;

case 5: insert_at_pos();

break;

case 6: delete_at_begin();

break;

case 7: delete_at_end();

break;

case 8: delete_at_pos();

break;

case 9: search();

break;

case 10: sort();

break;

case 11: count();

break;

case 12: reverse();

break;

case 13: merge();

break;

default:exit(1);

}

void create()

{

new=(struct node *)malloc(sizeof(struct node));

printf("enter a value");

scanf("%d",&value);

new->data=value;

new->next=NULL;

if(head==NULL)

{

head=new;

temp=new;

}

else

{

temp->next=new;

temp=temp->next;

}

printf("\n do u want to add one more node to the list(y/n)? ");

scanf("%c",&ch);

}while(ch=='y');

}

void display()

{

temp=head;

while(temp!=NULL)

{

printf("%d->",temp->data);

temp=temp->next;

}

void insert_at_begin()

{

new=(struct node *)malloc(sizeof(struct node));

printf("enter a value");

scanf("%d",&value);

new->data=value;

if(head == NULL)

{

new->next = NULL;

head = new;

}

else

{

new->next = head;

head = new;

}

printf("\nOne node inserted!!!\n");

}

void insert_at_end()

{

new=(struct node *)malloc(sizeof(struct node));

printf("enter a value");

scanf("%d",&value);

new->data=value;

new->next=NULL;

if(head == NULL)

head = new;

else

{

temp=head;

while(temp->next!=NULL)

{

temp=temp->next;

}

temp->next=new;

}

printf("\nOne node inserted!!!\n");

}

void insert_at_pos()

{

temp=head;

new=(struct node *)malloc(sizeof(struct node));

printf("enter a value");

scanf("%d",&value);

printf("enter a position");

scanf("%d",&p);

new->data=value;

if(head == NULL)

{

new->next = NULL;

head = new;

}

else

{

temp = head;

for(i=1;i<p-1;i++)

{

temp=temp->next;

}

new->next=temp->next;

temp->next=new;

}

printf("\nOne node inserted!!!\n");

}

void delete_at_begin()

{

if(head == NULL)

printf("\n\nList is Empty!!!");

else

{

temp = head;

if(head->next == NULL)

{

head = NULL;

free(temp);

}

else

{

temp = head;

printf("%d-> is deleted",head->data);

head=head->next;

temp->next=NULL;

free(temp);

}

void delete_at_end()

{

if(head == NULL)

{

printf("\nList is Empty!!!\n");

}

else

{

temp = head;

if(head->next == NULL)

head = NULL;

else

{

while(temp->next->next!=NULL)

{

temp=temp->next;

}

d=temp->next;

temp->next=NULL;

printf("End node is deleted");

free(d);

}

void delete_at_pos()

{

temp=head;

printf("enter a position");

scanf("%d",&p);

for(i=1;i<p-1;i++)

{

temp=temp->next;

}

d=temp->next;

temp->next=d->next;

printf("Node deleted Sucessfully");

d->next=NULL;

free(d);

}

void search()

{

int key,flag=0;

printf("enter the value to search");

scanf("%d",&key);

temp=head;

while(temp!=NULL)

{

if(key==temp->data)

{

flag+=1;

}

else

{

temp=temp->next;

}

if(flag==1)

{

printf(" found");

}

else

{

printf("not found");

}

void sort()

{

int temp;

struct node *temp1,*temp2;

for(temp1=head;temp1->next!=NULL;temp1=temp1->next)

{

for(temp2=head;temp2->next!=NULL;temp2=temp2->next)

{

if(temp2->data>temp1->data)

{

temp=temp2->data;

temp2->data=temp2->next->data;

temp2->next->data=temp;

}

void count()

{

int count=0;

temp=head;

while(temp!=NULL)

{

count=count+1;

temp=temp->next;

}

printf("\n number of nodes=%d",count);

}

void reverse()

{

struct node *prev=NULL,*current,*next;

current=head;

while(current!=NULL)

{

next=current->next;

current->next=prev;

prev=current;

current=next;

}

head=prev;

}

void merge()

{

int value;

struct node *head1=NULL;

{

new1=(struct node *)malloc(sizeof(struct node));

printf("enter a value");

scanf("%d",&value);

new1->data=value;

new1->next=NULL;

if(head1==NULL)

{

head1=new1;

temp1=new1;

}

else

{

temp1->next=new1;

temp1=temp1->next;

}

printf("\n do u want add one more node(y/n)");

scanf("%c",&ch);

}while(ch=='y');

temp=head;

while(temp->next!=NULL)

{

temp=temp->next;

}

temp->next=head1;

}

Advantages of linked list:- Or Advantages of Single linked list

1. Linked list is a dynamic data structure i.e. memory will be allocated at run time. So, no wastage of memory.

2. It is not necessary to know in advance regarding the number of elements to be stored in the list.

3. Insertion and deletion operations are easier, as shifting of values is not necessary.

4. Different types of data can be stored in data field of a node.

5. The memory allocation need not be in contiguous locations.

6. Linear data structures such as stacks, queues are easily implemented using linked list.

Disadvantages or limitations of single linked list:-

1. Random access of elements in not possible in single linked list i.e. we can’t access a particular node directly.

2. Binary search algorithm can’t be implemented on a single linked list.

3. There is no way to go back from one node to its previous node i.e. only forward traversal is possible.

4. Extra storage space for pointer is required.

5. Reversing single linked list is difficult.

Circular linked list:-

In a circular linked list, the last node contains a pointer to the first node of the list. We can have a circular singly linked list as well as a circular doubly linked list.

1) Circular Single Linked List: While traversing a circular Single linked list, we can begin at any node and traverse the list in any direction, forward or backward, until we reach the same node where we started. Thus, a circular linked list has no beginning and no ending.

Circular linked list is a linear data structure which contains a collection of nodes where each node contains 2 fields.

1. Data field:- It contains a value which may be an integer, float, char and string.

2. Next field:- It contains address of its next node. The last node next field contains address of first node.

2) Circular Doubly Linked List:

A circular doubly linked list or a circular two-way linked list is a more complex type of linked list which contains a pointer to the next as well as the previous node in the sequence

The difference between a doubly linked and a circular doubly linked list is same as that exists between a singly linked list and a circular linked list. The circular doubly linked list does not contain NULL in the previous field of the first node and the next field of the last node. Rather, the next field of the last node stores the address of the first node of the list, i.e., START. Similarly, the previous field of the first field stores the address of the last node.

Circular Linked list operations:- or Circular Linked list ADT

We can perform mainly the following operations on circular linked list.

1. Creation

2. Display

3. Inserting an element into the list at begin position

4. Inserting an element into the list at end position

5. Inserting an element into the list at specified position

6. Deleting an element from the list at begin position

7. Deleting an element from the list at end position

8. Deleting an element from the list at specified position

9. Counting the number of elements or nodes

C program to implement circular linked list:-

#include<stdio.h>

#include<stdlib.h>

void create();

void display();

void insert_at_begin();

void insert_at_end();

void insert_at_pos();

void delete_at_begin();

void delete_at_end();

void delete_at_pos();

void count();

struct node

{

int data;

struct node *next;

}*new,*head,*temp,*d;

int i,p,value;

char ch;

void main()

{

int n;

printf("\n 1.create\n 2.display\n 3.insert_at_begin\n 4.insert_at_end\n 5.insert_at_pos\n 6.delete_at_begin\n 7.delete_at_end\n 8.delete_at_pos\n 9.count");

while(1)

{

printf("enter ur choice");

scanf("%d",&n);

switch(n)

{

case 1:create();

break;

case 2:display();

break;

case 3:insert_at_begin();

break;

case 4:insert_at_end();

break;

case 5:insert_at_pos();

break;

case 6:delete_at_begin();

break;

case 7:delete_at_end();

break;

case 8:delete_at_pos();

break;

case 9:count();

break;

default:exit(1);

}

void create()

{

new=(struct node *)malloc(sizeof(struct node));

printf("enter a value");

scanf("%d",&value);

new->data=value;

new->next=new;

if(head==NULL)

{

head=new;

temp=new;

}

else

{

temp->next=new;

temp=new;

new->next=head;

}

printf("\n do u want add one more node(y/n)");

scanf("%c",&ch);

}while(ch=='y');

}

void display()

{

temp=head;

while(temp->next!=head)

{

printf("%d->",temp->data);

temp=temp->next;

}

printf("%d->",temp->data);

}

void insert_at_begin()

{

new=(struct node *)malloc(sizeof(struct node));

printf("enter a value");

scanf("%d",&value);

new->data=value;

temp=head;

while(temp->next!=head)

{

temp=temp->next;

}

temp->next=new;

new->next=head;

head=new;

}

void insert_at_end()

{

new=(struct node *)malloc(sizeof(struct node));

printf("enter a value");

scanf("%d",&value);

new->data=value;

temp=head;

while(temp->next!=head)

{

temp=temp->next;

}

temp->next=new;

new->next=head;

}

void insert_at_pos()

{

new=(struct node *)malloc(sizeof(struct node));

printf("enter a value");

scanf("%d",&value);

printf("enter a position");

scanf("%d",&p);

new->data=value;

temp=head;

for(i=1;i<p-1;i++)

{

temp=temp->next;

}

new->next=temp->next;

temp->next=new;

}

void delete_at_begin()

{

temp=head;

while(temp->next!=head)

{

temp=temp->next;

}

d=head;

printf("deleted node is %d",d->data);

head=head->next;

temp->next=head;

d->next=NULL;

free(d);

}

void delete_at_end()

{

temp=head;

while(temp->next->next!=head)

{

temp=temp->next;

}

d=temp->next;

printf("deleted node is %d",d->data);

d->next=NULL;

temp->next=head;

free(d);

}

void delete_at_pos()

{

printf("enter a position");

scanf("%d",&p);

temp=head;

for(i=1;i<p-1;i++)

{

temp=temp->next;

}

d=temp->next;

printf("deleted node is %d",d->data);

temp->next=d->next;

d->next=NULL;

free(d);

}

void count()

{

temp=head;

int c=0;

while(temp!=head)

{

c+=1;

temp=temp->next;

}

printf("number of node is %d",c);

}

Advantages of circular linked list:- It saves time when we have to go to the first node from the last node. But in double linked list we have to go through in between nodes.

Limitations of circular linked list:- It is not easy to reverse circular linked list.

Double linked list:-

A double linked list or a two-way linked list is a more complex type of linked list which contains a pointer to the next as well as the previous node in the sequence.

Therefore, it consists of three parts—data, a pointer to the next node, and a pointer to the previous node.

Double linked list is a linear data structure which contains a collection of nodes, where each node contains 3 fields.

1. prev field:- It is a pointer field which contains the address of its previous node. The first node prev field contains NULL value.

2. data field :- It contains a value which may be an integer, float, char and string.

3. next field:-It is a pointer field which contains the address of its next node. The last node next field contains NULL value.

In a single linked list only forward traversal is possible i.e. we can traverse from left to right only where as in a double linked list both forward traversal(Left to right) as well as backward traversal(Right to left) is possible.

Diagrammatic representation of circular linked list:-

In C, the structure of a double linked list can be given as,

struct node

{

struct node *prev;

int data;

struct node *next;

};

The PREV field of the first node and the NEXT field of the last node will contain NULL. The PREV field is used to store the address of the preceding node, which enables us to traverse the list in the backward direction.

Thus, we see that a double linked list calls for more space per node and more expensive basic operations. However, a double linked list provides the ease to manipulate the elements of the list as it maintains pointers to nodes in both the directions (forward and backward). The main advantage of using a double linked list is that it makes searching twice as efficient.

C program to implement Double linked list:-

#include<stdio.h>

#include<stdlib.h>

void create();

void display();

void insert_at_begin();

void insert_at_end();

void insert_at_pos();

void delete_at_begin();

void delete_at_end();

void delete_at_pos();

void reverse();

struct node

{

int data;

struct node *prev,*next;

}*new,*head,*temp,*d;

int i,value,p;

char ch;

void main()

{

int n;

printf("\n 1.create\n 2.display\n 3.insert_at_begin\n 4.insert_at_end\n 5.insert_at_pos\n 6.delete_at_begin\n 7.delete_at_end\n 8.delete_at_pos\n 9.reverse");

while(1)

{

printf("enter your choice:");

scanf("%d",&n);

switch(n)

{

case 1:create();

break;

case 2:display();

break;

case 3:insert_at_begin();

break;

case 4:insert_at_end();

break;

case 5:insert_at_pos();

break;

case 6:delete_at_begin();

break;

case 7:delete_at_end();

break;

case 8:delete_at_pos();

break;

case 9:reverse();

break;

default:exit(1);

}

void create()

{

new=(struct node *)malloc(sizeof(struct node));

printf("enter a value");

scanf("%d",&value);

new->prev=NULL;

new->data=value;

new->next=NULL;

if(head==NULL)

{

head=new;

temp=new;

}

else

{

new->prev=temp;

temp->next=new;

temp=temp->next;

}

printf("\n do u want add one more node(y/n)");

scanf("%c",&ch);

}while(ch=='y');

}

void display()

{

temp=head;

while(temp!=NULL)

{

printf("%d<->",temp->data);

temp=temp->next;

}

void insert_at_begin()

{

new=(struct node *)malloc(sizeof(struct node));

printf("enter a value");

scanf("%d",&value);

new->data=value;

new->next=head;

head->prev=new;

head=new;

}

void insert_at_end()

{

new=(struct node *)malloc(sizeof(struct node));

printf("enter a value");

scanf("%d",&value);

temp=head;

while(temp->next!=NULL)

{

temp=temp->next;

}

new->prev=temp;

temp->next=new;

new->data=value;new->next=NULL;

}

void insert_at_pos()

{

new=(struct node *)malloc(sizeof(struct node));

printf("enter a value");

scanf("%d",&value);

printf("enter a position");

scanf("%d",&p);

temp=head;

for(i=1;i<p-1;i++)

{

temp=temp->next;

}

new->next=temp->next;

temp->next->prev=new;

temp->next=new;

new->prev=temp;

new->data=value;

}

void delete_at_begin()

{

temp=head;

printf("\n deleted node is%d->",temp->data);

head=head->next;

temp->next=NULL;

head->prev=NULL;

free(temp);

}

void delete_at_end()

{

temp=head;

while(temp->next->next!=NULL)

{

temp=temp->next;

}

d=temp->next;

temp->next=NULL;

d->prev=NULL;

printf("\n deleted node is %d",d->data);

free(d);

}

void delete_at_pos()

{

temp=head;

printf("enter a position");

scanf("%d",&p);

for(i=1;i<p-1;i++)

{

temp=temp->next;

}

d=temp->next;

temp->next=d->next;

d->next->prev=temp;

printf("\n deleted node is %d",temp->data);

d->prev=NULL;

d->next=NULL;

free(d);

}

void reverse()

{

temp=head;

while(temp->next!=NULL)

{temp=temp->next;

}

while(temp->prev!=NULL)

{

printf("%d<->",temp->data);

temp=temp->prev;

}

printf("%d<->",temp->data);

}

Advantages of double linked list:-

1. We can traverse in both directions i.e. from left to right as well as from right to left.

2. It is easy to reverse a double linked list.

Limitations of double linked list:-

1. It requires more memory because one extra field (prev) is required.

2. Insertion and deletion operations takes more time because more operations are required.

C program to create a linear linked list of customer names and their telephone numbers. The program should be menu-driven and include features for adding a new customer, deleting an existing customer and for displaying the list of all customers.

#include<stdio.h>

#include<conio.h>

#include<string.h>

#include<alloc.h>

struct node

{

char cno[20];

char tno[20];

struct node *next;

}*head,*temp,*newnode;

int pos,i;

void create();

void dis();

void insert_at_begin();

void insert_at_end();

void insert_at_pos();

void delete_at_begin();

void delete_at_end();

void delete_at_pos();

main()

{

int ch;

while(1)

{

printf("\n********MENU*********\n");

printf("\n1.create\n2.display\n3.insert at begin\n4.insert at end\n5.insert at position\n6.delete at begin\n7.delete at end\n8.delete at position\n");

printf("enter your choice");

scanf("%d",&ch);

switch(ch)

{

case 1:

create();

break;

case 2:

dis();

break;

case 3:

insert_at_begin();

break;

case 4:

insert_at_end();

break;

case 5:

insert_at_pos();

break;

case 6:

delete_at_begin();

break;

case 7:

delete_at_end();

break;

case 8:

delete_at_pos();

break;

default:

exit(0);

}

getch();

}

void create()

{

char c,cname[20],tnum[20];

{

newnode=(struct node *)malloc(sizeof(struct node));

printf("enter customer id");

fflush(stdin);

scanf("%s",&newnode->cno);

printf("enter tel no");

fflush(stdin);

scanf("%s",&newnode->tno);

newnode->next=NULL;

if(head==NULL)

{

head=temp=newnode;

}

else

{

temp->next=newnode;

temp=newnode;

}

printf("do you want one more node?(y/n)");

fflush(stdin);

scanf("%c",&c);

}while(c=='y');

}

void dis()

{

printf("\n*****customer details******\n");

printf("\ncustomer no\ttel.number\n");

printf("__________________________\n");

temp=head;

while(temp!=NULL)

{

printf("%s\t%s",temp->cno,temp->tno);

printf("\n");

temp=temp->next;

}

void insert_at_begin()

{

newnode=(struct node *)malloc(sizeof(struct node));

printf("enter customer no and tel no");

fflush(stdin);

gets(newnode->cno);

fflush(stdin);

gets(newnode->tno);

newnode->next=head;

head=newnode;

}

void insert_at_end()

{

newnode=(struct node *)malloc(sizeof(struct node));

printf("enter customer no and tel no");

fflush(stdin);

gets(newnode->cno);

fflush(stdin);

gets(newnode->tno);

temp=head;

while(temp->next!=NULL)

temp=temp->next;

temp->next=newnode;

newnode->next=NULL;

}

void insert_at_pos()

{

newnode=(struct node *)malloc(sizeof(struct node));

printf("enter position");

scanf("%d",&pos);

printf("enter customer no and tel no");

fflush(stdin);

gets(newnode->cno);

fflush(stdin);

gets(newnode->tno);

temp=head;

for(i=0;i<pos-2;i++)

{

temp=temp->next;

}

newnode->next=temp->next;

temp->next=newnode;

}

void delete_at_begin()

{

temp=head;

head=head->next;

temp->next=NULL;

}

void delete_at_end()

{

temp=head;

while(temp->next->next!=NULL)

temp=temp->next;

temp->next=NULL;

}

void delete_at_pos()

{

printf("enter position");

scanf("%d",&pos);

temp=head;

for(i=0;i<pos-2;i++)

temp=temp->next;

temp->next=temp->next->next;

}

Linked list applications:-

1.Polynomials can be represented and various operations can be performed on polynomials using linked lists.

2.Sparse matrix can be represented using linked list.

3.Various details like student details, customer details , product details and so on can be implemented using linked list.

Search This Blog

Pappula Sarala

Data Structures UNIT I

Example 2

Algorithm: Traverse/Display:

Inserting Elements to a Linked List:

1. Insert a Node at the beginning of a Linked list:

Algorithm: InsertAtBeginning

2. Insert a Node at the end of a Linked list:

Algorithm: InsertAtEnd

3. Insert a Node after a given Node in a Linked list:

Algorithm: InsertAnElementAtSpecificLocation

Deleting Elements from a Linked List

1. Delete a Node from the beginning of a Linked list:

Algorithm: DeleteFromBeginning

2. Delete last Node from a Linked list:

Algorithm: DeleteFromEnd

3. Delete the Node after a given Node in a Linked list:

Algorithm: DeleteAfterANode

Comments

Post a Comment

Popular posts from this blog

Data Structures Module_V

Data Structures Module-IV

DS - Module - II - DLL